Processing

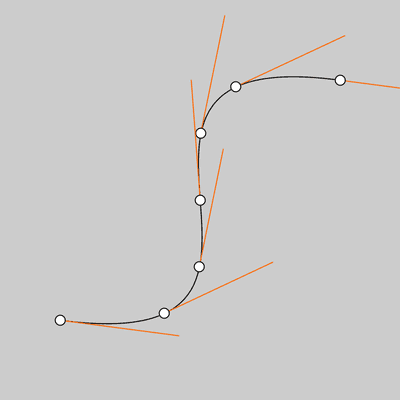
size(400,400);
noFill();
bezier(340, 80, 40, 40, 360, 360, 60, 320);

int steps = 6;
fill(255);
for (int i = 0; i <= steps; i++) {
  float t = i / float(steps);
  // Get the location of the point
  float x = bezierPoint(340, 40, 360, 60, t);
  float y = bezierPoint(80, 40, 360, 320, t);
  // Get the tangent points
  float tx = bezierTangent(340, 40, 360, 60, t);
  float ty = bezierTangent(80, 40, 360, 320, t);
  // Calculate an angle from the tangent points
  float a = atan2(ty, tx);
  a += PI;
  stroke(255, 102, 0);
  line(x, y, cos(a)*120 + x, sin(a)*120 + y);
  // The following line of code makes a line 
  // inverse of the above line
  //line(x, y, cos(a)*-30 + x, sin(a)*-30 + y);
  stroke(0);
  ellipse(x, y, 10, 10);
}

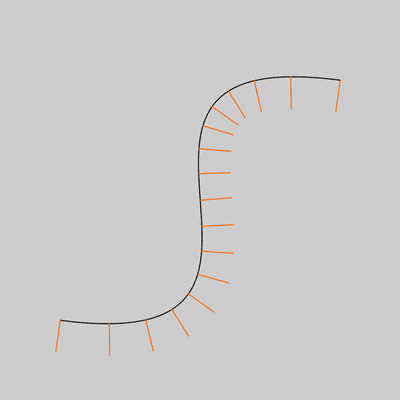
size(400,400);

noFill();
bezier(340, 80, 40, 40, 360, 360, 60, 320);
stroke(255, 102, 0);
int steps = 16;
for (int i = 0; i <= steps; i++) {
  float t = i / float(steps);
  float x = bezierPoint(340, 40, 360, 60, t);
  float y = bezierPoint(80, 40, 360, 320, t);
  float tx = bezierTangent(340, 40, 360, 60, t);
  float ty = bezierTangent(80, 40, 360, 320, t);
  float a = atan2(ty, tx);
  a -= HALF_PI;
  line(x, y, cos(a)*32 + x, sin(a)*32 + y);
}